The Influence of Display type on Decision Making
The way an operator thinks about displayed values may depend on whether the display format is digital or analogue (pointer and scale).
The results suggest the operator does arithmetic calculations on digital displays, and absolute judgement - into a category of value relative to a context - on analogue displays. So the best display type may depend on the type of cognitive processing needed.
The suggestions here are based on analysis of verbal protocols from a process control task.
This paper illustrates a type of detailed analysis which can be done when a verbal protocol contains several instances of the same sub-task.
Notes not in original paper in [ ].
Main sections :
Task definitions of control error, summary of operator's methods.
Detailed example of how an operator's method of deciding on level of control error is identified from their verbal protocol.
How operator decides on size of control action in response to error.
The Influence of Display type on Decision Making
Lisanne Bainbridge
Department of Psychology, University of Reading
Institute of Electrical Engineers Conference Publication No. 80, Displays, 1971, pp. 209-215.
Many studies of display reading performance are made in a context where the task investigated is that of reading the display. In real contexts the task is to use the displayed data in making some decision.
Display reading studies concentrate on the accuracy with which a display can be read. This emphasis on accuracy can lead to the assumption that decisions using the displayed data are also made with high accuracy. This paper provides evidence on some of the ways in which process control operators use data in making control decisions, and how the type of display may influence the way its data are used. The evidence suggests that the decisions actually make use of rough estimates of data value, so that studies of absolute judgement (the category assessment of quantitative variables) is more appropriate in considering decision making performance than studies of high levels of digital accuracy.
The task studied (see Bainbridge et al, 1968) was that of controlling electric power supply in a digital simulation of 5 electric-arc steel-melting furnaces. The computer was also used to log display and control variable values. The operators, all experienced furnace men, were asked to 'think aloud' while controlling. These reports ('protocols') were tape-recorded and transcribed. There is a photograph of the operator interface in Bainbridge et al op cit Figure 1.
The log of display and control values shows what control changes the operator made (his output) and the context in which they were made (his input). The traditional method of analysing control performance is to find correlations between input and output. The protocols provide additional data on the operator's decisions relating input and output. In this task there are three parts :
1. Identifying the control error,
2. Selecting the particular furnace to alter,
3. Selecting the size of control action.
The second decision is non-numerical, this paper will discuss the quantitative stages, 1 and 3. As input and output considerations are separated by a qualitative decision they can be studied separately here, though this distinction may not occur in other tasks.
Definition of Control Error
The operator has to control the allocation of power to the furnaces so that they do not use more than 50 MWh altogether in a given half-hour period. [The furnaces use a huge amount of power, and local power generation does not want the demand to be completely unpredictable.] The operator does not control the operation of the furnaces themselves, though when he cuts the power supplied to them he does affect their steel-making efficiency, so he attempts to use the full 50 MWh.
Two definitions of the control error at a given time in the 1/2 hr are available :
1. Constant Target Value : A simple method of achieving the above aim would be to maintain the momentary power usage (P) at 50 MW throughout the 1/2 hr, i.e. Control error = P - 50.
2. Corrected Target Value : Because of differences in furnaces and in stages of the steel making process it is not possible to obtain P = 50 at all times. A more sophisticated strategy allows for this by calculating the target Power usage value which can be used during the rest of the 1/2 hr., given the MWh used so far.
Various versions of this calculation give the same answer, for instance it can be based on power used so far or on power still available. Each uses the variables : P, time now, and MWh used so far.
Figure 1 : Corrected control error [target value] and action size.
[Dotted line shows action size = error size.]
Numbers indicate sequence of actions by S22.
As individual operators use different tolerances and gains in their control it would too confusing to present group data, so example data from one subject [S22, an experienced melting shop manager] are given throughout. This operator's control changes are correlated with error relative to corrected target value, as shown in Figure 1, so he is using the second definition of error. The verbal protocol data also support this, as the operator explicitly mentions values of the 3 variables necessary.
bottom of table shows the measures mentioned by S22 during different time periods.]
During the first 5 minutes of each 1/2 hr. he mentions only P, as shown in [the bottom of] Table 1. This suggests that he may start by using the simpler first definition, which would be efficient as too little power has been used to make correcting that target value worthwhile.
[From 6-14 minutes he mentions the variables used in calculating corrected control value from MWh used so far.
In the final 1/4 hour he mentions the variables used in calculating corrected control value from MWh to go.]
Identifying Control Error
Evidence on how the operator makes the required computation can be obtained from the protocol.
Table 2 analyses a sequence of 4 phrases in the protocol from this melting-shop manager.
This illustrates two technical points about analysing this type of material.
The protocol often does not mention the name of the variable for which a value is quoted, but this can be found by checking with the log-sheet.
Although computations are not mentioned, to be able to make certain numerical statements the operator must have carried out certain computations, so these can be inferred.
This sequence also provides an example to illustrate the main point about the way the operator computes.
1. Where numerical values are given, the underlying computations are made in a sequence of steps each involving 2 operands.
2. The 'MWh used so far' display gives values to 2 decimal places, however computations such as in phrase 2 are reported to the nearest whole number, see Table 3.
Table 3
[MWh : x < x.9, S22 rounds down.
MWh : x.9 < x < x.99, S22 rounds up.]
3. Operations connecting phrases 3 and 4 in Table 2 must be inferred.
As mentioned above [the control error - action size link is not direct], the operator must go on from identifying a control error to choosing a furnace to make the corrective action on. This non-numerical decision does not depend on the size of the control error, but is determined by whether or not an action is needed immediately, and whether this should increase or decrease the present power usage. These are categories of control state, so the operator must find the control error and then assign it to one of these categories.
If the processing continues in the same way as in phrases 1-3 [in Table 2], the full sequence underlying the above phrases should be as shown in the following figure. This operator does not ever mention steps 4 and 5 of this sequence. Also, while steps 1 and 2 frequently occur in his protocol, step 3 only occurs twice, and in both cases the arithmetic involved is easy.
Figure 2 : Sequence of underlying steps in identifying the control state (above, below, etc.)
[phrase numbers in Table 2]
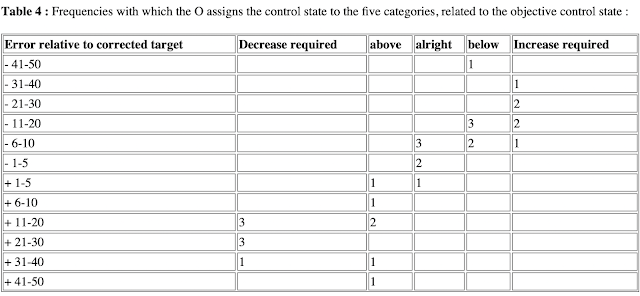
Analysis of protocol phrases about the control state, as in phrase 4 in Table 2 (step 6 in Figure 2), shows that the operator does divide the error variable into 5 overlapping bands: power cut required, power above target, power usage acceptable, power below target, power increase required, as discussed above, see Table 4 below. The process by which this is done is not mentioned in the protocol, but some suggestions can be made, for which later analysis gives better evidence.
Table 4
[left - objective control error, identified by experimenter from event record at time when S22 made comment,
right - frequency of comments made by S22 when control error is at this level]
The 3 displayed variables used in the calculations in Figure 2 are :
time now, and MWh used so far [steps 1 and 2], which are shown on digital displays,
and present power usage, P [step 5], on a pointer-plus-dial analogue display.
In this example, and throughout the protocol, operations directly using digitally displayed values, as in steps 1 and 2 [in figure 2], are explicitly calculated numerically.
Other operations, making further computations using the number obtained, e.g. steps 3 and 4, or using variables shown on dial displays, e.g. step 5, are never mentioned explicitly, only the final category response is quoted.
This allows the possibility that these calculations are made by some mental analogue process rather than numerically. Of course, if the operator does not mention a numerical calculation explicitly, this does not necessarily mean that he has not made this calculation. However, if the operator shows no evidence in his later actions or protocol of having available the accurate result of such a calculation, one assumes it has not been made.
It would be simpler for an operator to use the analogue of the pointer position when a variable is presented on a dial, rather than converting this spatial position into a numerical value and then using this in a digital calculation. This amount of 'effort' or time involved in obtaining an answer may generally be an important factor. An analogue computation can be made quickly, in one time unit, while a digital calculation is made in a series of steps, so takes longer. Although human operators' analogue computations are inaccurate (see later) they would be favoured in any situation where there are time pressures. (There is also evidence that operators differ in the amount to which they use them.)
Calculating size of action
This is a proportional control task with unit gain :
cutting power supply to a furnace by x MW reduces the total power usage by x MW.
An added complexity is that power supply to a given furnace cannot be varied continuously, only 4 discrete settings are available, at 0, 50, 75 and 100 % of the maximum power required.
As this maximum requirement varies with the furnace and the stage in the steel-making process, the operator must compute the effect in MW of making a particular control setting change, for accurate control decision making. Two predictions about this computation can be made from the previous discussion. A furnaces's present power usage is displayed by pointer-plus-dial, so analogue computation might be used. Also a discrete result is given so there might be a categorising effect. Both these are supported. The operator illustrated above suggests a new percentage power setting without previous explicit mention of furnace power usage in 8 out of 12 actions, and without calculation in 11 of the actions.
For accurate control, as discussed, the operator has to work out the effect of a control setting before its efficiency can be tested. Before he can do this he must choose a control setting to work out the effect of, and he can only do this by some judgement process, which presumably must be analogue. This means the operator could use a strategy of simply making the action chosen by judgement without calculating its effect accurately, in a spirit of trial-and-error. This interpretation is supported by the data. For instance the above operator makes some remark such as 'well, let's try that anyway' before 4 out of 7 of his groups of actions, and all of those have to be followed by further actions. He apparently controls by making some approximate change and checking and correcting its effect.
Further evidence of analogue computation can be given. If the operator is making a digital calculation of control error, and digital comparison of this with action size, his control actions must be the same size as the error, or inversely if they are not the same size he cannot be calculating numerically. The data show that at the beginning of the test run the actions are consistently about half the size of the error, but tend towards the correct size at the end of the run, see Figure 1. The operator must be making rough, or inaccurate, analogue computations, and corrects his gain with experience. [The operators were experienced steel men but they were working on a simulator of an unfamiliar task.]
Conclusion
This analysis has suggested various influences on the process by which an operator makes control computations, all of which require further test. The computations may be digital or analogue, and this may be influenced by the type of display on which the relevant variables are presented.
In addition computations may not be made using a continuous analogue but using a few discrete steps, or category values, where the aim is to identify a discrete setting or qualitative category.
Categorisation is a necessary stage in the present task. It would be interesting to know whether operators of any slow control task use such a descriptive or 'perceptual' stage in their control activity.
This particular task also has implications for panel design, as it points to the difficulties caused when an operator has to make intermediate computations as part of his control activities. The display/ control compatibility problems of digital displays, discrete control settings, and intermediate calculations could usefully be studied.
-
Reference
Bainbridge, L., Beishon, J., Hemming, J.H. and Splaine, M. (1968) A study of real-time decision-making using a plant simulator. Operational Research Quarterly, Special Conference Issue, 19, 91-106.
reprinted in Edwards, E. and Lees, F.P. (eds.) The Human Operator in Process Control, Taylor & Francis, London. pp. 91-104.
Collection of the data described in this paper was supported by a grant from the Human Factors Committee of the British Iron and Steel Research Association, under the direction of Dr. R. J. Beishon, and using facilities provided in Sheffield by the then United Steel Companies Limited.
©2021 Lisanne Bainbridge








Comments
Post a Comment